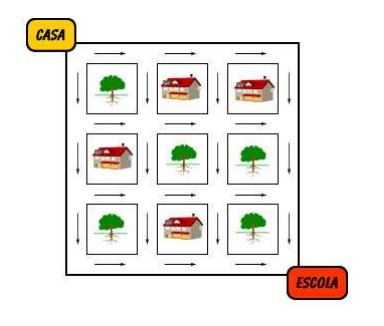
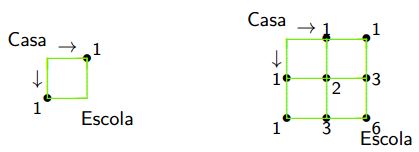Comece por olhar para o caso em que existe apenas um ou dois blocos de casas entre os pontos de partida e de destino:
No primeiro caso existem 2 caminhos distintos entre a casa e a escola. Agora observe que, no segundo caso, o número de caminhos possíveis para chegar a cada esquina é igual à soma do número de caminhos possíveis para chegar a cada uma das esquinas adjacentes. Os números indicam de quantas maneiras se pode chegar a cada vértice. Continuando pelo mesmo processo podemos completar a contagem. Assim, o meu Miguel pode ir para a escola através de 20 caminhos diferentes.
[toggle title=”Para pensar”]
- Existem diferentes caminhos com o mesmo comprimento?
- Qual o comprimento do caminho mais curto de casa do Miguel até à escola?
- De quantas maneiras pode o Miguel ir para a escola, se no caminho quiser passar na casa do seu amigo Manel, que fica no ponto A?
- Porque é importante para as companhias de transportes a escolha de caminhos eficientes?
[/toggle]
[toggle title=”Curiosidades”]
Blaise Pascal foi um matemático Francês do século XVII, que trabalhou com um padrão de números para resolver vários problemas de contagem. Este padrão, conhecido como triângulo de Pascal, forma-se começando com linhas de 1’s em dois lados de um triângulo e somando os dois números acima, à esquerda e à direita, para obter cada novo número do padrão.
[/toggle]